Функция Askley:

Функция ASKLEY имеет следующий вид:

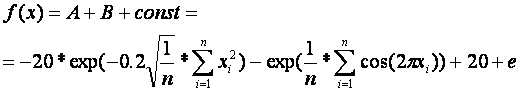
где :

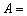
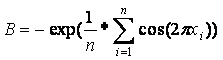
C = 20+e, вводится для удобства визуализации, чтобы получался ноль в оптимуме.

В рассматриваемом примере n=30, xi=-30 +30 .

Оптимум (минимум) достигается при xi* =0, i=130, целевая функция F(x*) =0.

Особенность этой задачи в том, что переменных достаточно много n=30, имеется огромное число локальных экстремумов, визуализация даже при двух переменных из-за масштаба отображения многого не показывает. Поэтому не получается достоверного отображения. Но главное то, что составляющие А и В несоизмеримы в большинстве точек пространства, вероятность быть соизмеримыми сопоставима с числом . Если одновременно все xi близки к нулю или хотя бы близки к единице, то соизмеримость достигается. Дело не в оптимизационном алгоритме! Если бы компьютер держал бы в памяти числовую информацию до 200 десятичных знаков (по мантиссе), то проблем не возникало бы. А реально получается так, что на фоне 8 байт (15 десятичных знаков) составляющая "А" просто "не видна".

Тем не менее, разработанный нами алгоритм легко находит это решение, правда, если решать эту задачу в целочисленных понятиях. В этой связи приводим программу ASKLEY_ZEL.exe

Эта же задача решается и в непрерывных понятиях. В диапазоне xi=-30 +30 получается не верное решение, приводящее к F(x*) =20, смотри ASKLEY_NEPR.exe. В диапазоне xi=-3 +3 (смотри ASKLEY_NEPR_3.exe), получается правильное решение. Если ввести в память генетического алгоритма точку с небольшими значениями координат, то проблем вообще не возникает, как не решай эту задачу(смотри ASKLEY_NEPR+1.exe) .

Так как используется "ГЕНЕТИКА" в составе "ДИСО" (смотри теоретическую часть), то надо в диалоге ДОС - окна сначала выбрать режим - нажать клавишу "2", а затем ответить опять - "2" (здесь разницы не будет, можно и - "1").

На самом деле, функция ASKLEY несколько проще, составляющая А имеет следующее выражение:

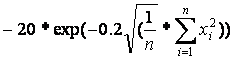, то есть

Материалы для скачивания: