 |
|
| Главная страница | |
| Теория | |
| Описание системы | |
| Тестирование | |
| - Решение тестов | |
| - Содержание тестов | |
| Оценка работоспособности | |
| Технология работы | |
|
|
| Перечень методов | |
| Теория | |
| Технология работы | |
| Оценка работоспособности | |
|
Решение собственных задач |
| FORTRAN (CVF) | |
| Произвольный язык программирования | |
|
Учебный процесс |
Здесь выполняется исследование на тестовой функции "Растригин"
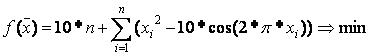
-50<xi<50, i=1,n
Оптимальное решение:
xi*=(0,0,…..0), f*=0.
Тест проходит при n=500. Это очень много!
Рассматривается несколько методов решения этой задачи.
1. Как целочисленная задача
В этом случае каждая переменная принимает 100 целых значений от -50 до +50. Тогда число всевозможных вариантов задачи составляет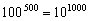 
. Как видно из расчета, необходимо 1792 итерации работы генетической оптимизации, а число реализаций модели в этом случае составляет
2. Как последовательность "искусственных" целочисленных задач
В этом случае n-мерное пространство (500-мерное по тесту) разбивается по каждой переменной на "m" равномерно распределенных дискретных значений, из которых строятся решения. Общее число вариантов составит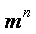 
. В тесте рассмотрен случай m=10, n=500. Получив решение, можно продолжить эту процедуру неограниченное число раз, уточняя каждый раз решение (реализация глобальности поиска при этом сохраняется ! ), однако в примере это не требуется, так как сразу получается абсолютный результат.
Дополнительные вспомогательные файлы показывают диапазоны нахождения оптимума по переменным вначале и после окончания очередного этапа поиска (файлы Z_NEPR_ZEL и Z_NEPR_ZEL _old).
3. Как обычная непрерывная задача
Сходимость здесь значительно ниже, так как количество вариантов бесконечно. Так, например, время реализации 195000 итераций составило что-то порядка 2-3 часов. При этом результат постоянно вначале явно, а затем мене заметно улучшался. Приводим несколько уже полученных сокращенных вариантов такого анализа (текстовые файлы 1.37.txt, 3.52.txt, 0.0235.txt, где число соответствует найденному значению целевой функции, хотя точное значение - "ноль"). Во все перечисленных расчетах модель рассчитывалась 200000-340000 раз. Определенное расхождение при анализе итераций (порядок "движения" целевой функции) обусловлено разными диапазонами управляемых переменных ( в одних расчетах было -50 - +50 в других -5 - +5)
Результативность оптимизации связана с количеством управляемых переменных, поэтому приводим результаты по данной тестовой функции для самого трудоемкой схемы генетической оптимизации - непрерывной в случае 5, 50, 150, 500 переменных в отдельном doc - файле: Растригин 5_50_150_500.doc.
Материалы для скачивания:
