






Задача коммивояжера
1. Состояние вопроса
2. Решение задачи коммивояжера на плоскости
2.1 Координаты объектов,
полученные датчиком случайных чисел
2.2 Визуализация координат объектов
2.3 Исходная ситуация при оптимизации на минимум генетическим алгоритмом
2.4 Лучший вариант по максимуму, найденный случайно-генетическим алгоритмом
2.5 Абсолютно лучший вариант по максимуму, найденный методом «ближайшего соседа»
2.6 Один из лучших вариантов по минимуму, найденный случайно-генетическим алгоритмом
2.7 Абсолютно лучший вариант по минимуму, найденный методом «ближайшего соседа»
2.8 Выборочные результаты оптимизации на минимум случайно-генетическим алгоритмом
3. Решение задачи коммивояжера на окружности
1. Состояние вопроса
Задача коммивояжера относится к классу трудно решаемых задач (NP- полные задачи), причем никакой алгоритм не гарантирует поиск оптимального решения, разве что полный перебор. Как известно, количество вариантов составляет n! (для 40 пунктов это число равно1,121576252666462*1076, для 100 пунктов – 9,332621544394418*10157). Вполне понятно, даже суперкомпьютер не способен просчитать эти варианты за сколько-нибудь обозримое время и даже100-1000 лет здесь ничтожно мало.
Некоторые авторы утверждают, что задача коммивояжера является лучшей для тестирования генетических алгоритмов. Мы придерживаемся другой точки зрения – оптимизация (математическая) предполагает некоторую упорядоченность, взаимосвязь цели и принимаемых решений; задача коммивояжера с позиций оптимизации это состояние хаоса, где перебор неизбежен. Только специальные алгоритмы, эвристики в какой то мере эффективны. Так, например, метод «ближайшего соседа» при равномерном расположении объектов является чрезвычайно эффективным.
Тем не менее,
всякий оптимизационный алгоритм полезно проверить на этой задаче. Не
представляет исключения в этом плане и генетический алгоритм с элементами
случайного поиска, который в большей мере соответствует традиционному
оптимизационному подходу, в отличие от специальных алгоритмов поиска. Решая эту
задачу как оптимизационную, необходимо каким-то образом управляемые параметры (![]() ) связать
с объектами – маршрутом. Здесь мало уметь генерировать случайные целые числа,
необходимо, чтобы они не повторялись бы и были бы не зависимыми. Это можно
достичь, если генерировать как обычно случайные числа, связав их с исходной
целочисленной последовательностью – номерами маршрута, и выполняя сортировку по
возрастанию/ убыванию случайных чисел и
связанных с ними номеров.
) связать
с объектами – маршрутом. Здесь мало уметь генерировать случайные целые числа,
необходимо, чтобы они не повторялись бы и были бы не зависимыми. Это можно
достичь, если генерировать как обычно случайные числа, связав их с исходной
целочисленной последовательностью – номерами маршрута, и выполняя сортировку по
возрастанию/ убыванию случайных чисел и
связанных с ними номеров.
В качестве тестов можно взять прямую, окружность, плоскость со случайно расположенными точками. В первых двух случаях ответ известен (расчет сводится к определению расстояния между двумя точками и определению длины окружности), для третьего теста можно получить оценку по методу «ближайшего соседа». Более того, целесообразно решить задачу в обратном направлении – максимизация длины маршрута; тогда можно судить об эффективности поиска, даже если оптимальное решение в точности не известно. Очевидно, тест с прямой проще, в большей мере соответствует традиционной оптимизации: между координатами точек, длиной прямой линии и маршрутом просматривается устойчивое соответствие, которое будет обнаружено оптимизацией и приведет к успеху. Алгоритм, компьютер «не видит» этих фигур. Если визуализировать оптимальный маршрут и он в действительности будет таковым, то полученные фигуры должны напоминать прямую и окружность соответственно, а плоскость можно контролировать по плотности и длине отдельных линий – составляющих маршрута движения. Впрочем, подобные суждения ассоциируются уже с элементами искусственного интеллекта.
2. Решение задачи коммивояжера на плоскости
Объекты
маршрута в количестве 100 штук расположены случайно в квадрате с границами в
диапазоне -50 ![]() 50. Задача решалась методом «ближайшего соседа» (БС), который
специально разработан под данную задачу и
универсальным оптимизационным методом – случайно-генетическим алгоритмом
(СГА). Решение выполнялось как на максимум, так и на минимум, что позволило
оценить диапазон качества принимаемых решений. Максимум по СГА составил 7802.255
единиц, по БС - 8004.537 единиц. При решении на
минимум 957.954 единиц и 866.610
соответственно. То есть диапазон составил 8004.537 - 866.610 единиц в
абсолютной шкале измерений и 823,7% в
относительной шкале измерений ((8004.537 - 866.610)/ 866.610 = 8.237). Вполне
понятно, что точное решение при такой размерности не известно, получить его
просто не представляется возможным! Оценка отклонения по цели (на min) составило 10,54% ((957.954 - 866.610)/ 866.610 * 100%).
50. Задача решалась методом «ближайшего соседа» (БС), который
специально разработан под данную задачу и
универсальным оптимизационным методом – случайно-генетическим алгоритмом
(СГА). Решение выполнялось как на максимум, так и на минимум, что позволило
оценить диапазон качества принимаемых решений. Максимум по СГА составил 7802.255
единиц, по БС - 8004.537 единиц. При решении на
минимум 957.954 единиц и 866.610
соответственно. То есть диапазон составил 8004.537 - 866.610 единиц в
абсолютной шкале измерений и 823,7% в
относительной шкале измерений ((8004.537 - 866.610)/ 866.610 = 8.237). Вполне
понятно, что точное решение при такой размерности не известно, получить его
просто не представляется возможным! Оценка отклонения по цели (на min) составило 10,54% ((957.954 - 866.610)/ 866.610 * 100%).
2.1 Координаты объектов,
полученные датчиком случайных чисел
1 x = -0.49998E+02 y = 0.41497E+02
2 x = 0.39161E+02 y = 0.46796E+02
3 x = 0.14976E+01 y = -0.10199E+02
4 x = 0.24351E+02 y = 0.41045E+02
5 x = 0.82230E+01 y = -0.30957E+02
6 x = 0.11713E+01 y = -0.37663E+02
7 x = 0.22621E+02 y = 0.46661E+02
8 x = -0.73949E+01 y = -0.39950E+02
9 x = 0.40153E+02 y = 0.46153E+02
10 x = 0.35799E+02 y = 0.40684E+02
11 x = 0.43624E+02 y = -0.85355E+01
12 x = 0.14893E+01 y = 0.10457E+02
13 x = 0.18914E+02 y = -0.44273E+01
14 x = -0.40637E+02 y = 0.10948E+02
15 x = 0.99549E+01 y = 0.34493E+02
16 x = 0.27285E+02 y = -0.42834E+02
17 x = -0.27639E+02 y = 0.28037E+02
18 x = -0.31866E+02 y = -0.11670E+02
19 x = 0.23931E+02 y = -0.18587E+02
20 x = -0.88015E+01 y = -0.40889E+02
21 x = 0.77058E+01 y = 0.33608E+02
22 x = -0.16515E+02 y = -0.44218E+01
23 x = -0.37120E+02 y = -0.32548E+02
24 x = -0.46270E+02 y = 0.41633E+00
25 x = 0.79016E+01 y = 0.17411E+02
26 x = -0.43330E+02 y = 0.33270E+02
27 x = -0.30914E+02 y = 0.33460E+02
28 x = 0.49080E+02 y = 0.38644E+02
29 x = 0.12225E+02 y = -0.17265E+02
30 x = 0.87706E+01 y = -0.34910E+02
31 x = 0.29894E+02 y = -0.93045E+01
32 x = -0.22828E+02 y = -0.30205E+02
33 x = -0.10363E+02 y = 0.40407E+02
34 x = 0.13256E+02 y = -0.37491E+02
35 x = -0.41115E+02 y = -0.44886E+02
36 x = -0.45740E+02 y = -0.49973E+01
37 x = -0.15455E+01 y = -0.34503E+01
38 x = -0.27746E+02 y = 0.29382E+02
39 x = -0.38499E+02 y = 0.10457E+02
40 x = 0.19800E+02 y = 0.25597E+02
41 x = -0.45865E+02 y = -0.32635E+02
42 x = 0.25149E+02 y = 0.10662E+02
43 x = 0.63480E+01 y = -0.25310E+02
44 x = -0.18095E+02 y = -0.32844E+02
45 x = 0.28041E+02 y = 0.35245E+02
46 x = 0.29263E+02 y = -0.45243E+02
47 x = 0.28363E+02 y = -0.29438E+02
48 x = -0.49059E+02 y = 0.34708E+02
49 x = 0.26129E+02 y = 0.20441E+02
50 x = 0.59919E+01 y = -0.34712E+02
51 x = 0.41144E+02 y = 0.18998E+02
52 x = 0.48258E+02 y = 0.43636E+02
53 x = -0.27779E+02 y = 0.51436E+01
54 x = -0.19649E+02 y = 0.41745E+02
55 x = -0.26398E+02 y = 0.30192E+02
56 x = 0.48381E+02 y = 0.11381E+02
57 x = 0.34161E+02 y = 0.26020E+02
58 x = -0.39530E+02 y = -0.44909E+02
59 x = -0.32123E+02 y = -0.21407E+01
60 x = -0.17002E+02 y = -0.59895E+01
61 x = 0.20728E+02 y = 0.47786E+02
62 x = 0.23509E+02 y = 0.13798E+02
63 x = -0.46580E+02 y = 0.45053E+02
64 x = 0.72538E+01 y = 0.48179E+02
65 x = -0.43137E+02 y = 0.31163E+02
66 x = 0.47919E+02 y = -0.19271E+02
67 x = 0.31654E+02 y = 0.93630E+01
68 x = 0.11905E+02 y = -0.48332E+02
69 x = -0.31215E+02 y = -0.41599E+02
70 x = -0.46351E+02 y = -0.17015E+01
71 x = 0.23514E+02 y = -0.40364E+02
72 x = -0.32401E+02 y = 0.18021E+02
73 x = -0.32558E+02 y = 0.17182E+02
74 x = -0.10543E+02 y = -0.24845E+02
75 x = -0.11084E+02 y = 0.31673E+02
76 x = -0.24250E+02 y = -0.26813E+02
77 x = 0.31905E+02 y = -0.30350E+02
78 x = -0.35871E+02 y = 0.16484E+02
79 x = 0.40851E+02 y = 0.30183E+02
80 x = -0.34410E+02 y = -0.25195E+02
81 x = -0.19928E+02 y = -0.24427E+02
82 x = 0.49398E+02 y = 0.20123E+02
83 x = 0.41117E+02 y = 0.34735E+02
84 x = -0.43062E+02 y = -0.39532E+02
85 x = 0.20655E+02 y = -0.49185E+02
86 x = -0.60347E+01 y = -0.81231E+00
87 x = -0.48297E+02 y = -0.36434E+02
88 x = -0.25077E+02 y = 0.13801E+02
89 x = 0.34350E+02 y = -0.19839E+02
90 x = -0.29314E+02 y = -0.32097E+02
91 x = 0.45742E+02 y = 0.10561E+02
92 x = -0.35754E+02 y = -0.29909E+02
93 x = -0.28616E+02 y = 0.26880E+01
94 x = -0.13828E+02 y = 0.84057E+01
95 x = 0.46406E+02 y = -0.47211E+02
96 x = -0.25740E+02 y = 0.94173E+01
97 x = 0.23562E+02 y = 0.44020E+02
98 x = 0.96257E+01 y = -0.42032E+02
99 x = -0.38355E+02 y = -0.16847E+02
100 x = -0.19596E+02 y = 0.25477E+01
2 x = 0.39161E+02 y = 0.46796E+02
3 x = 0.14976E+01 y = -0.10199E+02
4 x = 0.24351E+02 y = 0.41045E+02
5 x = 0.82230E+01 y = -0.30957E+02
6 x = 0.11713E+01 y = -0.37663E+02
7 x = 0.22621E+02 y = 0.46661E+02
8 x = -0.73949E+01 y = -0.39950E+02
9 x = 0.40153E+02 y = 0.46153E+02
10 x = 0.35799E+02 y = 0.40684E+02
11 x = 0.43624E+02 y = -0.85355E+01
12 x = 0.14893E+01 y = 0.10457E+02
13 x = 0.18914E+02 y = -0.44273E+01
14 x = -0.40637E+02 y = 0.10948E+02
15 x = 0.99549E+01 y = 0.34493E+02
16 x = 0.27285E+02 y = -0.42834E+02
17 x = -0.27639E+02 y = 0.28037E+02
18 x = -0.31866E+02 y = -0.11670E+02
19 x = 0.23931E+02 y = -0.18587E+02
20 x = -0.88015E+01 y = -0.40889E+02
21 x = 0.77058E+01 y = 0.33608E+02
22 x = -0.16515E+02 y = -0.44218E+01
23 x = -0.37120E+02 y = -0.32548E+02
24 x = -0.46270E+02 y = 0.41633E+00
25 x = 0.79016E+01 y = 0.17411E+02
26 x = -0.43330E+02 y = 0.33270E+02
27 x = -0.30914E+02 y = 0.33460E+02
28 x = 0.49080E+02 y = 0.38644E+02
29 x = 0.12225E+02 y = -0.17265E+02
30 x = 0.87706E+01 y = -0.34910E+02
31 x = 0.29894E+02 y = -0.93045E+01
32 x = -0.22828E+02 y = -0.30205E+02
33 x = -0.10363E+02 y = 0.40407E+02
34 x = 0.13256E+02 y = -0.37491E+02
35 x = -0.41115E+02 y = -0.44886E+02
36 x = -0.45740E+02 y = -0.49973E+01
37 x = -0.15455E+01 y = -0.34503E+01
38 x = -0.27746E+02 y = 0.29382E+02
39 x = -0.38499E+02 y = 0.10457E+02
40 x = 0.19800E+02 y = 0.25597E+02
41 x = -0.45865E+02 y = -0.32635E+02
42 x = 0.25149E+02 y = 0.10662E+02
43 x = 0.63480E+01 y = -0.25310E+02
44 x = -0.18095E+02 y = -0.32844E+02
45 x = 0.28041E+02 y = 0.35245E+02
46 x = 0.29263E+02 y = -0.45243E+02
47 x = 0.28363E+02 y = -0.29438E+02
48 x = -0.49059E+02 y = 0.34708E+02
49 x = 0.26129E+02 y = 0.20441E+02
50 x = 0.59919E+01 y = -0.34712E+02
51 x = 0.41144E+02 y = 0.18998E+02
52 x = 0.48258E+02 y = 0.43636E+02
53 x = -0.27779E+02 y = 0.51436E+01
54 x = -0.19649E+02 y = 0.41745E+02
55 x = -0.26398E+02 y = 0.30192E+02
56 x = 0.48381E+02 y = 0.11381E+02
57 x = 0.34161E+02 y = 0.26020E+02
58 x = -0.39530E+02 y = -0.44909E+02
59 x = -0.32123E+02 y = -0.21407E+01
60 x = -0.17002E+02 y = -0.59895E+01
61 x = 0.20728E+02 y = 0.47786E+02
62 x = 0.23509E+02 y = 0.13798E+02
63 x = -0.46580E+02 y = 0.45053E+02
64 x = 0.72538E+01 y = 0.48179E+02
65 x = -0.43137E+02 y = 0.31163E+02
66 x = 0.47919E+02 y = -0.19271E+02
67 x = 0.31654E+02 y = 0.93630E+01
68 x = 0.11905E+02 y = -0.48332E+02
69 x = -0.31215E+02 y = -0.41599E+02
70 x = -0.46351E+02 y = -0.17015E+01
71 x = 0.23514E+02 y = -0.40364E+02
72 x = -0.32401E+02 y = 0.18021E+02
73 x = -0.32558E+02 y = 0.17182E+02
74 x = -0.10543E+02 y = -0.24845E+02
75 x = -0.11084E+02 y = 0.31673E+02
76 x = -0.24250E+02 y = -0.26813E+02
77 x = 0.31905E+02 y = -0.30350E+02
78 x = -0.35871E+02 y = 0.16484E+02
79 x = 0.40851E+02 y = 0.30183E+02
80 x = -0.34410E+02 y = -0.25195E+02
81 x = -0.19928E+02 y = -0.24427E+02
82 x = 0.49398E+02 y = 0.20123E+02
83 x = 0.41117E+02 y = 0.34735E+02
84 x = -0.43062E+02 y = -0.39532E+02
85 x = 0.20655E+02 y = -0.49185E+02
86 x = -0.60347E+01 y = -0.81231E+00
87 x = -0.48297E+02 y = -0.36434E+02
88 x = -0.25077E+02 y = 0.13801E+02
89 x = 0.34350E+02 y = -0.19839E+02
90 x = -0.29314E+02 y = -0.32097E+02
91 x = 0.45742E+02 y = 0.10561E+02
92 x = -0.35754E+02 y = -0.29909E+02
93 x = -0.28616E+02 y = 0.26880E+01
94 x = -0.13828E+02 y = 0.84057E+01
95 x = 0.46406E+02 y = -0.47211E+02
96 x = -0.25740E+02 y = 0.94173E+01
97 x = 0.23562E+02 y = 0.44020E+02
98 x = 0.96257E+01 y = -0.42032E+02
99 x = -0.38355E+02 y = -0.16847E+02
100 x = -0.19596E+02 y = 0.25477E+01
2.2 Визуализация координат объектов
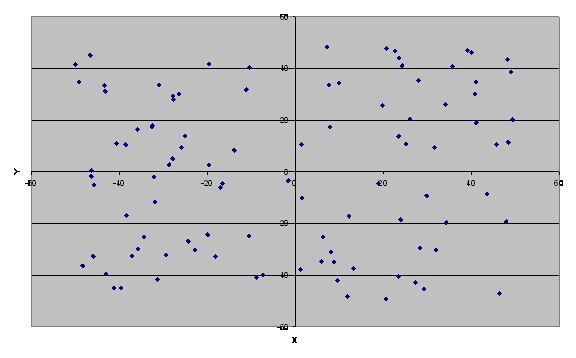
2.3 Исходная ситуация при оптимизации на минимум генетическим алгоритмом
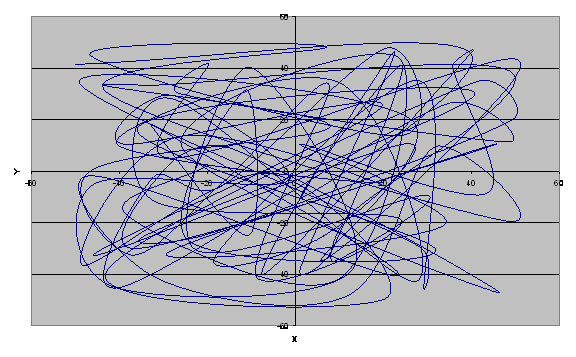
Рис.2 - Исходная ситуация при оптимизации на минимум генетическим алгоритмом : S=4681.997 ( это значение получено методом случайного поиска на первом этапе оптимизации)
2.4 Лучший вариант по максимуму, найденный случайно-генетическим алгоритмом
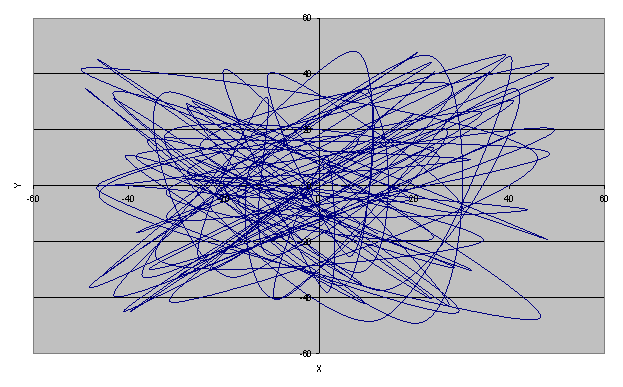
Рис.3 - Лучший вариант по
максимуму, найденный случайно-генетическим алгоритмом : длина пути S= 7802.255
2.5 Абсолютно лучший вариант по максимуму, найденный методом «ближайшего соседа»
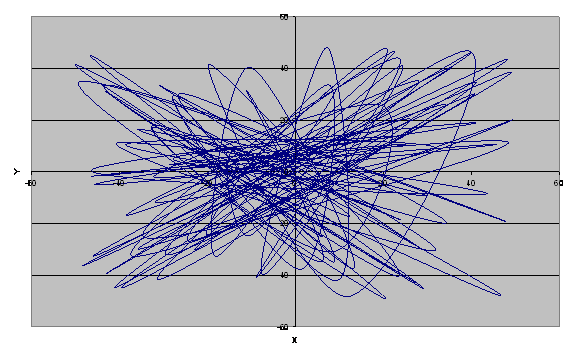
Рис.4 - Абсолютно лучший вариант по максимуму, найденный методом «ближайшего соседа» : длина пути S= 8004.537
2.6 Один из лучших вариантов по минимуму, найденный случайно-генетическим алгоритмом
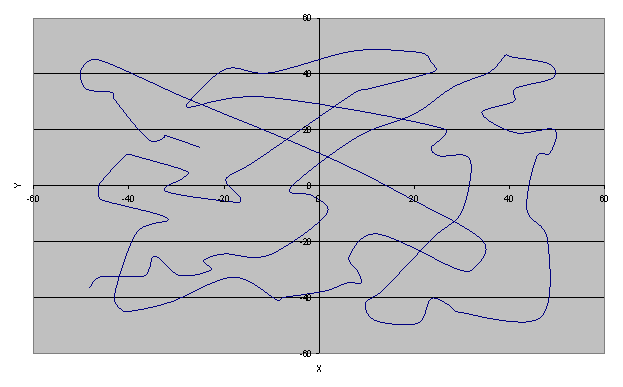
Рис.5 - Один из лучших вариантов, найденный случайно-генетическим алгоритмом : длина пути S=970.171 (лучшему варианту соответствует S=957.954)
2.7 Абсолютно лучший вариант по минимуму, найденный методом «ближайшего соседа»
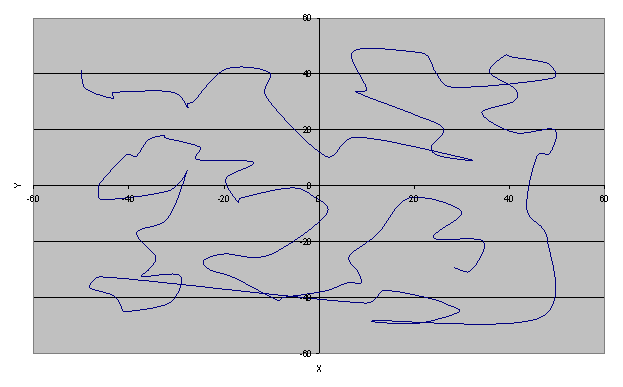
Рис.5 - Абсолютно лучший вариант, найденный методом
«ближайшего соседа» : длина пути S=866.610
2.8 Выборочные результаты оптимизации на минимум случайно-генетическим алгоритмом
1 итерация значение целевой функции - 4681.99735773696
значение параметра области сходимости - 84.1185253495350
201 итерация значение целевой функции - 2560.48236136636
значение параметра области сходимости - 0.276744943789864
401 итерация значение целевой функции - 2240.37342980292
………………………………………………………………………………….
3601 итерация значение целевой функции - 1425.47430076493
………………………………………………………………………………….
5001 итерация значение целевой функции - 1315.56604687016
………………………………………………………………………………….
18801 итерация значение целевой функции - 1108.02656803611
………………………………………………………………………………….
34401 итерация значение целевой функции - 1079.22829613919
………………………………………………………………………………….
70201 итерация значение целевой функции - 1061.65241658885
………………………………………………………………………………….
100201 итерация значение целевой функции - 959.011699832533
………………………………………………………………………………….
117401 итерация значение целевой функции - 957.954044212779
………………………………………………………………………………….
обращений к модели - 2326157
значение параметра области сходимости - 84.1185253495350
201 итерация значение целевой функции - 2560.48236136636
значение параметра области сходимости - 0.276744943789864
401 итерация значение целевой функции - 2240.37342980292
………………………………………………………………………………….
3601 итерация значение целевой функции - 1425.47430076493
………………………………………………………………………………….
5001 итерация значение целевой функции - 1315.56604687016
………………………………………………………………………………….
18801 итерация значение целевой функции - 1108.02656803611
………………………………………………………………………………….
34401 итерация значение целевой функции - 1079.22829613919
………………………………………………………………………………….
70201 итерация значение целевой функции - 1061.65241658885
………………………………………………………………………………….
100201 итерация значение целевой функции - 959.011699832533
………………………………………………………………………………….
117401 итерация значение целевой функции - 957.954044212779
………………………………………………………………………………….
обращений к модели - 2326157
Маршрут
28 52 9 2 10 97
7 61 64 4 45 83
79 57 51 82 56 91
11 66 89 77 16 71
34 50 74 81 76 32
90 58 35 23 92 80
41 87 84 69 44 20
8 6 29 13 31 67
42 62 49 40 15 21
25 19 47 95 46 85
68 98 30 5 43 3
37 86 12 75 33 54
27 55 38 17 72 73
96 53 93 18 99 39
14 24 70 36 59 60
22 100 94 88 78 65
26 48 1 63
Координаты
28 x = 0.49080E+02 y = 0.38644E+02
52 x = 0.48258E+02 y = 0.43636E+02
9 x = 0.40153E+02 y = 0.46153E+02
2 x = 0.39161E+02 y = 0.46796E+02
10 x = 0.35799E+02 y = 0.40684E+02
97 x = 0.23562E+02 y = 0.44020E+02
7 x = 0.22621E+02 y = 0.46661E+02
61 x = 0.20728E+02 y = 0.47786E+02
64 x = 0.72538E+01 y = 0.48179E+02
4 x = 0.24351E+02 y = 0.41045E+02
45 x = 0.28041E+02 y = 0.35245E+02
83 x = 0.41117E+02 y = 0.34735E+02
79 x = 0.40851E+02 y = 0.30183E+02
57 x = 0.34161E+02 y = 0.26020E+02
51 x = 0.41144E+02 y = 0.18998E+02
82 x = 0.49398E+02 y = 0.20123E+02
56 x = 0.48381E+02 y = 0.11381E+02
91 x = 0.45742E+02 y = 0.10561E+02
11 x = 0.43624E+02 y = -0.85355E+01
66 x = 0.47919E+02 y = -0.19271E+02
89 x = 0.34350E+02 y = -0.19839E+02
77 x = 0.31905E+02 y = -0.30350E+02
16 x = 0.27285E+02 y = -0.42834E+02
71 x = 0.23514E+02 y = -0.40364E+02
34 x = 0.13256E+02 y = -0.37491E+02
50 x = 0.59919E+01 y = -0.34712E+02
74 x = -0.10543E+02 y = -0.24845E+02
81 x = -0.19928E+02 y = -0.24427E+02
76 x = -0.24250E+02 y = -0.26813E+02
32 x = -0.22828E+02 y = -0.30205E+02
90 x = -0.29314E+02 y = -0.32097E+02
58 x = -0.39530E+02 y = -0.44909E+02
35 x = -0.41115E+02 y = -0.44886E+02
23 x = -0.37120E+02 y = -0.32548E+02
92 x = -0.35754E+02 y = -0.29909E+02
80 x = -0.34410E+02 y = -0.25195E+02
41 x = -0.45865E+02 y = -0.32635E+02
87 x = -0.48297E+02 y = -0.36434E+02
84 x = -0.43062E+02 y = -0.39532E+02
69 x = -0.31215E+02 y = -0.41599E+02
44 x = -0.18095E+02 y = -0.32844E+02
20 x = -0.88015E+01 y = -0.40889E+02
8 x = -0.73949E+01 y = -0.39950E+02
6 x = 0.11713E+01 y = -0.37663E+02
29 x = 0.12225E+02 y = -0.17265E+02
13 x = 0.18914E+02 y = -0.44273E+01
31 x = 0.29894E+02 y = -0.93045E+01
67 x = 0.31654E+02 y = 0.93630E+01
42 x = 0.25149E+02 y = 0.10662E+02
62 x = 0.23509E+02 y = 0.13798E+02
49 x = 0.26129E+02 y = 0.20441E+02
40 x = 0.19800E+02 y = 0.25597E+02
15 x = 0.99549E+01 y = 0.34493E+02
21 x = 0.77058E+01 y = 0.33608E+02
25 x = 0.79016E+01 y = 0.17411E+02
19 x = 0.23931E+02 y = -0.18587E+02
47 x = 0.28363E+02 y = -0.29438E+02
95 x = 0.46406E+02 y = -0.47211E+02
46 x = 0.29263E+02 y = -0.45243E+02
85 x = 0.20655E+02 y = -0.49185E+02
68 x = 0.11905E+02 y = -0.48332E+02
98 x = 0.96257E+01 y = -0.42032E+02
30 x = 0.87706E+01 y = -0.34910E+02
5 x = 0.82230E+01 y = -0.30957E+02
43 x = 0.63480E+01 y = -0.25310E+02
3 x = 0.14976E+01 y = -0.10199E+02
37 x = -0.15455E+01 y = -0.34503E+01
86 x = -0.60347E+01 y = -0.81231E+00
12 x = 0.14893E+01 y = 0.10457E+02
75 x = -0.11084E+02 y = 0.31673E+02
33 x = -0.10363E+02 y = 0.40407E+02
54 x = -0.19649E+02 y = 0.41745E+02
27 x = -0.30914E+02 y = 0.33460E+02
55 x = -0.26398E+02 y = 0.30192E+02
38 x = -0.27746E+02 y = 0.29382E+02
17 x = -0.27639E+02 y = 0.28037E+02
72 x = -0.32401E+02 y = 0.18021E+02
73 x = -0.32558E+02 y = 0.17182E+02
96 x = -0.25740E+02 y = 0.94173E+01
53 x = -0.27779E+02 y = 0.51436E+01
93 x = -0.28616E+02 y = 0.26880E+01
18 x = -0.31866E+02 y = -0.11670E+02
99 x = -0.38355E+02 y = -0.16847E+02
39 x = -0.38499E+02 y = 0.10457E+02
14 x = -0.40637E+02 y = 0.10948E+02
24 x = -0.46270E+02 y = 0.41633E+00
70 x = -0.46351E+02 y = -0.17015E+01
36 x = -0.45740E+02 y = -0.49973E+01
59 x = -0.32123E+02 y = -0.21407E+01
60 x = -0.17002E+02 y = -0.59895E+01
22 x = -0.16515E+02 y = -0.44218E+01
100 x = -0.19596E+02 y = 0.25477E+01
94 x = -0.13828E+02 y = 0.84057E+01
88 x = -0.25077E+02 y = 0.13801E+02
78 x = -0.35871E+02 y = 0.16484E+02
65 x = -0.43137E+02 y = 0.31163E+02
26 x = -0.43330E+02 y = 0.33270E+02
48 x = -0.49059E+02 y = 0.34708E+02
1 x = -0.49998E+02 y = 0.41497E+02
63 x = -0.46580E+02 y = 0.45053E+02
длина пути = 957.954044212779
3. Решение задачи коммивояжера на окружности
Объекты маршрута расположены случайно с центром в точке с координатами (0,0) на окружности радиуса 50 единиц. Вполне понятно, что оптимальный маршрут не превосходит 314,159 единиц. Многократные запуски исследуемого алгоритма дали следующие результаты: 448, 487, 514, 537, 568, 591 … Оптимизация на максимум приводит к результатам близким к числу 9340. Время счета каждого варианта занимало от 0,5 часа до 2 часов. Увы, оптимальный вариант найти не удалось! Большее время счета привело бы только к улучшению результата, но по, всей видимости, это существенно не изменило бы общей картины. Эксперименты данной задачи при 40 точках в шести случаях из 10-15 привели к точному оптимальному решению.
Если оптимизацию не выполнять, то маршрут движения подобен тому, что изображено на следующем рисунке 6 ( длина пути составляет 5322.8 единиц).
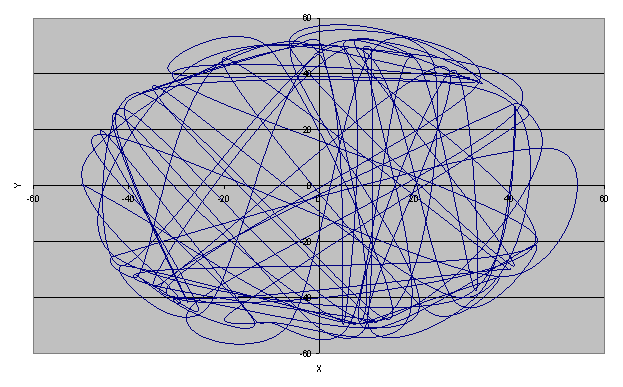
Рис.6 – Вместо движения по окружности, происходят беспорядочные движения, «компьютер не видит окружности»
Далее приводится визуализация решений данной задачи при 100 точках, соответствующих результату 448, 487 и 514 единиц. Результату около 314 единиц соответствовала бы окружности (на дисплее компьютера – эллипс).
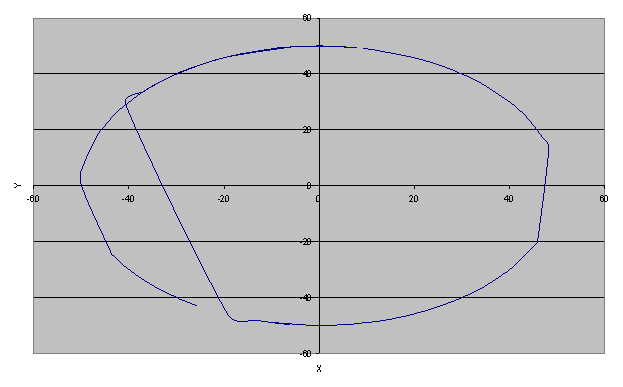
Рис.7 – Данному маршруту соответствует путь S = 448 единиц

Рис.8 – Данному маршруту соответствует путь S = 487 единиц
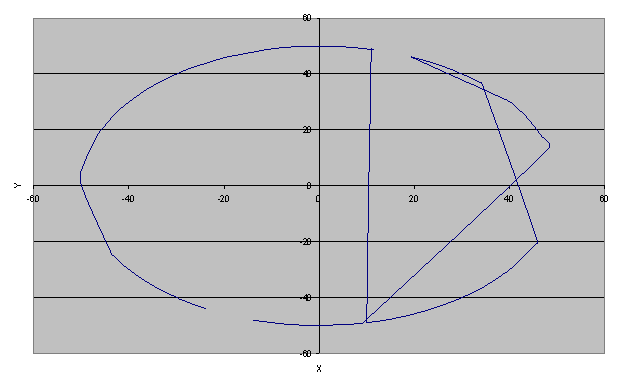
Рис.9 – Данному маршруту соответствует путь S = 514 единиц
